Teaching Division for Conceptual Understanding: The Five Reasons we Divide

Why do we learn about division in school? If you’ve spent any time teaching division, you may have wondered if it’s worth all the trouble.

It’s fair to wonder if division helps our students lead more successful and fulfilling lives…or whether they learn it to pass a test, and then move on.

And if we’re talking about memorizing division facts or simply calculating quotients, it’s a fair question. I believe our students would be just fine if we completely eliminated long division from the curriculum. Students won’t need it for advanced math, as they’ll have access to a calculator. And most will never use it in their lives out of school.

In the “real world,” no one uses long division to calculate quotients. We either divide in our heads, or use the calculators on our phones. But long division barely scratches the surface of the real importance of teaching division.

Teaching Division for Conceptual Understanding

It’s true that long division is mostly a waste of time. And a source of unnecessary frustration for many students and teachers. But that doesn’t mean we should stop teaching division altogether. 

It’s important for students to develop a conceptual understanding of division. An understanding of the meaning of division provides a foundation upon which students build more advanced, division-related concepts, such as fractions, proportions, and so on. 

Conceptual understanding also helps students remember what they learn (retention), and allows them to apply that understanding to real world scenarios, including word problems.

One way to teach for conceptual understanding is to highlight the connections between division and the other basic operations (especially multiplication). Teachers and students should also use visual and/or physical representations to represent division scenarios.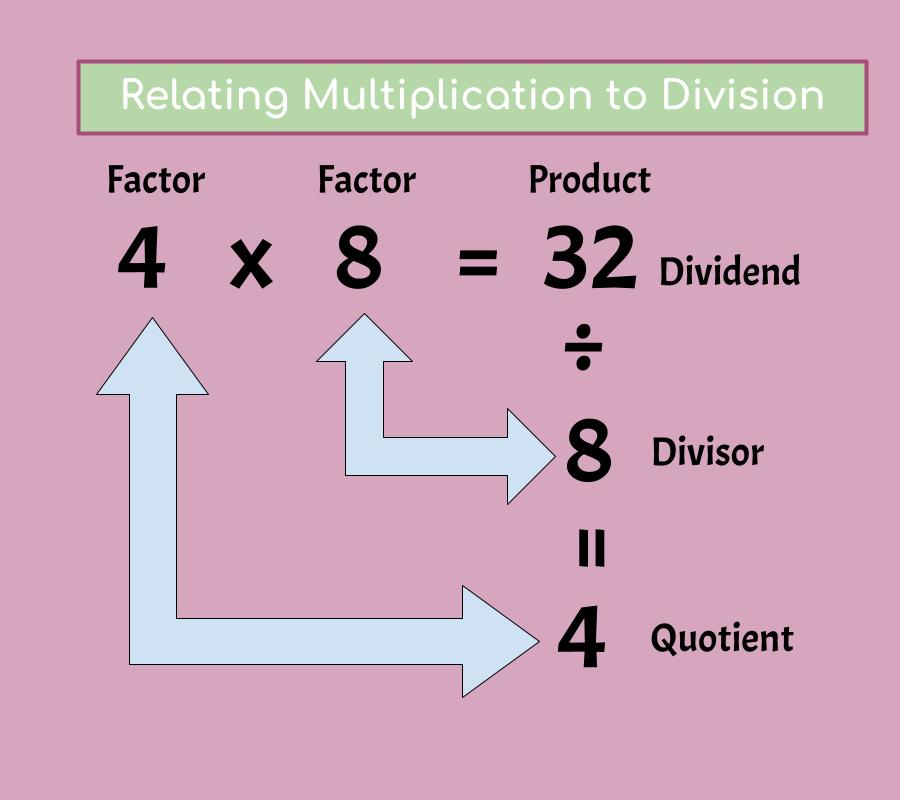

But teaching division effectively is not easy. Our lessons on division are often the first time students are exposed to algebraic reasoning. Addition, subtraction, and multiplication all allow students to start with one number, “do something to it,” and find a solution.

But to divide, they need to “work backward.” When dividing 24 by 8, for example, they need to find out the “unknown factor” (variable) that we can multiply by 8 to equal 24.

This quirk about teaching division is the reason why so many students struggle. And it’s why division is the only standard algorithm that uses the weird “house,” instead of just stacking one number on top of the other.

Why We Divide: The Five Meanings of Division

Teaching division is further complicated by the fact that there isn’t just one meaning of division, there are five. The Five Meanings of Division are the five reasons we divide. They help us understand why division was invented in the first place, and how we can use it on the world outside the classroom.

I was first exposed to the idea that there were just five meanings of multiplication in Chapter 4 of Math Matters by Suzanne Chapin and Art Johnson. I’ve written previously about how to use these Five Meanings to teach multiplication. If you haven’t seen that post yet, it may be helpful to read it before the rest of this article. 

Given the challenges unique to division, I thought it would be helpful to write an article specifically about how the Five Meanings of Multiplication apply to teaching division.

First off, it’s important to note that the meanings of division are not “ways to divide.” 

There are many ways to perform division, from visual modeling, to partial products, to long division. And let’s not forget the calculator. I’m sure there are literally dozens of division methods I’ve never heard of.

But the reasons we divide are different. They provide answers to the age-old questions, “Why do we have to learn this?” and “Will I ever use this outside of school.”

Being able to answer these questions is critical for establishing relevance, a critical ingredient in student motivation. Teaching students the meanings of division is also essential for developing conceptual understanding, and all the benefits that go along with such meaningful learning.

However, we don’t teach students all of the meanings at once. I’ve actually changed the order from Chapin & Jonson’s book, to better reflect the order in which students learn each meaning. 

Meaning #1: Equal Groups

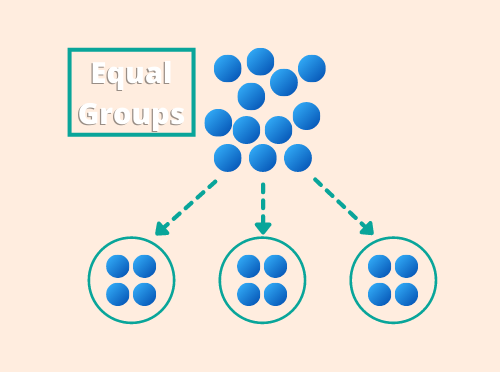
Most students are first exposed to division around 2nd or 3rd grade, through equal groups, or sharing.

We might present a situation where there are 12 cookies (dividend) and 3 friends (divisor). Students must find out how many cookies each friend gets (quotient). 

The reason for this meaning of division is fairly obvious. We all have times where we need to split something equally among a group of people. We’ve probably all had to split a check at a restaurant, or share a plate of apple slices with a friend.

Most of us instinctively perform this type of division by splitting into a set number of groups. When we hear “24 divided by 6” we think of 24 objects split into 6 groups, each of which has 4 items. In this case, the divisor tells us “how many groups,” and our quotient answers the question, “how many in each group.” This is known as partitive division.

But it’s important for students to learn that they can also perform an equal share with quotative division. This means that the divisor tells us “how many in each group.” So in the above example, we could put 6 objects in each group. And our quotient would answer the question, “how many groups.”

Quotative division is used for both long division and partial quotients. It also makes a lot more sense when dividing by a fraction. When students struggle with any of these, it can often be traced to unfamiliarity with quotative division.

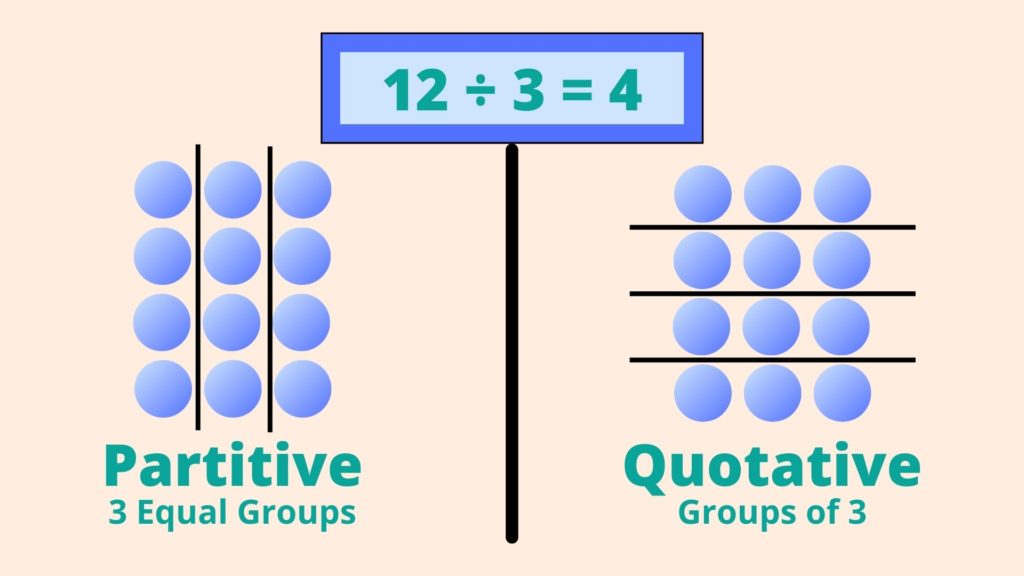The distinction between partitive and quotative applies to three of the meanings of division: equal groups, scaling, and rates. Known as asymmetrical multiplication/division, it means that the divisor and quotient (or the two factors) are different things, such as number of groups vs group size.

Meaning #2: Rectangular Array

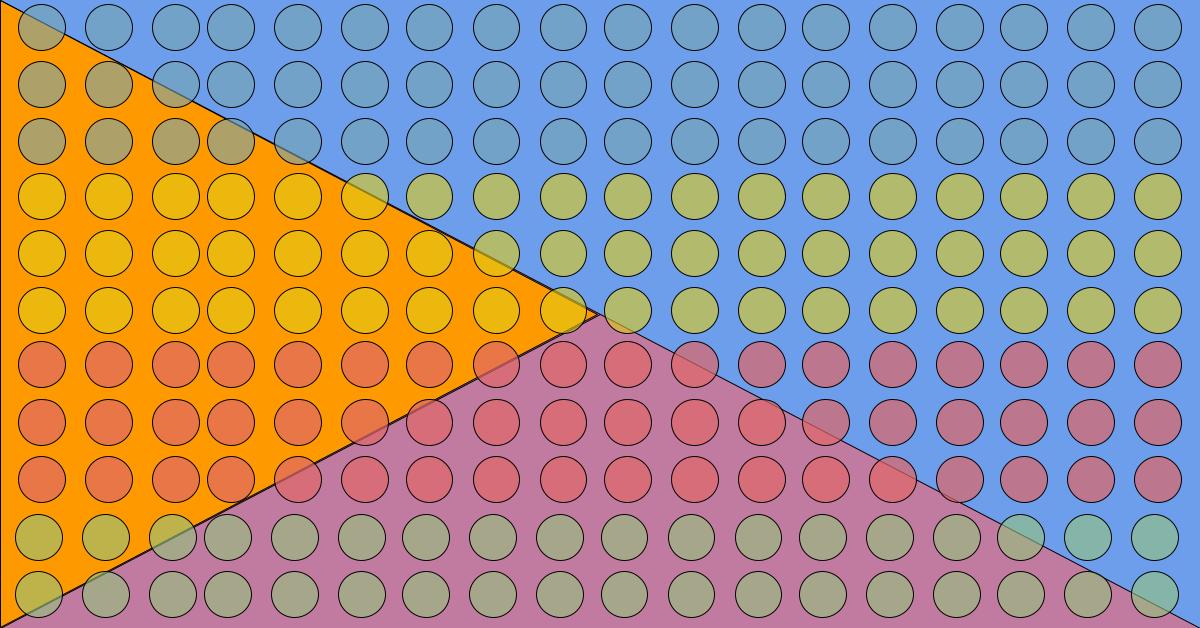
The next meaning of division students encounter is the rectangular array. Like equal groups, arrays (objects arranged in rows and columns) and area (the measurement of a 2-dimensional space) are typically introduced in 2nd or 3rd grade. 

Both are commonly used as tools for teaching multiplication, but applied less often for division. 

To turn an array from a multiplication to a division problem, think of the product (total number of objects) as a dividend. Then, one factor (eg, number of rows) becomes our divisor, and the other factor (eg, number of columns) is our quotient.

For example, we can give students a group of 15 counters (dividend) and ask them to create an array with 3 rows. 

The same can be done with area. If a hallway has an area of 500 sq ft, and a width of 10 ft, the length can be found by dividing.

Unlike equal groups, rectangular arrays are symmetrical, because the divisor and quotient are the same type of units. When dividing an area, the width and length are both in feet. 

Arrays may seem different (rows vs columns), but both are actually measured in terms of the ‘number of objects.’ Another way to think about it is that if you rotate an array, the rows become the columns. If you were to rotate a model of equal groups, the size of groups would not be interchangeable with the number of groups.

Meaning #3: Scaling (Multiplicative Comparison) 

In scaling problems, students explore situations where one group is ‘x times larger’ than the other. Multiplicative compare problems are introduced in 4th grade, and applied to scaling with fractions in 5th. 

Scaling becomes especially significant in middle school, as many concepts central to the MS curriculum, such as ratios, proportions, and percents all build on this concept.

As with arrays, the easiest way to understand scaling is to work back from a multiplication problem. If Jenae has 3 times as much money as Devin, we would multiply Devin’s money by 3 to find Jenae’s. But if we know how much Jenae has, but not Devin, we divide Jenae’s wealth by 3.

Scalar division can also be applied to situations where we multiply by a fraction. So if you plant tomatoes in ⅓ of your 50 sq. yard garden, we can divide by 3 to find the area in use.

In both cases, the divisor and quotient use different units – one is the scale factor and the other is the scaled size of the starting value – making scaling an example of asymmetrical division.

Students are often challenged by these problems because they confuse them with additive comparisons. If I have 5 times as many apples as someone with 10 apples, they may think I have 15 apples (adding 5).

The idea of “scaling” a number is also just more abstract than equal groups or rectangular arrays. It’s important for students to use visual and physical models, so they can ‘see’ and ‘feel,’ what’s actually happening when we scale.

Meaning #4: Rates 

Rates are another important meaning of division.

Rates are particularly interesting (and challenging), because each rate problem contains two examples of division.

First is the rate itself. To determine that my car travels 60 miles per hour, I take the total number of miles driven, and divide by the number of hours. 

We typically reduce rates to a ‘unit rate.’ For example, if I drove 300 miles over 5 hours, I would describe the rate as 60 mi/hr. This is considered a unit rate, because it describes how far I travel in 1 hour.

Because there is no divisor or denominator, it may not look like division or a fraction. But the ‘/’ between the units (miles and hours) reveals the division hidden in the rate.

To understand how division applies to a rate problem, we again work back from the multiplication. If you get paid an hourly rate of $20/hour, and work for 5 hours, you would earn $100.

If instead we start with your total earnings, and know that you worked 5 hours, we can divide to find your hourly rate. 

And if we knew that you earned $20/hour and your total earnings ($100), we would divide to find the hours you worked.

Because our divisors and quotients can be either your hourly rate or your hours worked, rates are another example of asymmetrical division. 

Meaning #5: Combinations (Cartesian Product) 

While combinations may be introduced for enrichment at the elementary level, they are primarily used in higher math.

A cartesian product is the number of possible ways we can combine two (or more) sets of numbers, objects, etc. Since 

These are usually introduced with multiplication examples such as, “If you have 3 shirts and 5 pairs of pants, how many different combinations of shirts and pants can you make?”

But if we know the number combinations and the size of one set, we use division to find the size of the other set. As illustrated in the graphic, if we have 3 shirts and can make 15 shirt-pant combinations, we divide to find the number of pants we have.

Combinations become useful when working with probabilities. To find the probability of an event, we first need to find the total possible outcomes. For example, a roll of two dice can produce a number from 2-12.

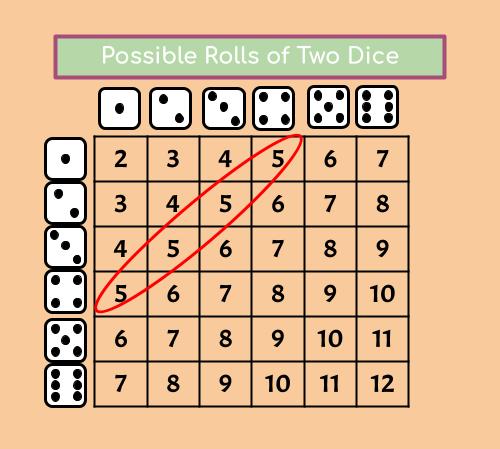But each number is not equally likely. To find the probability of each, first we need to find the total combinations by multiplying the possible outcomes for one die (6), by the possible outcomes for the other (also 6). 

Next, we would count the total ways we could roll, a 5 for example (4 ways), and divide by the total possibilities (36). This tells us there is a 1/9 chance (about 14%) of rolling a 5. (This second part of the process is actually a ‘scaling’ problem, with the probability being the scale factor).

Cartesian products are so named for their application to the Cartesian Plane, used for graphing x-y coordinates. Each ordered pair in the plane is a combination of a number from the x-axis with a number from the y-axis. 

They are also used in advanced applications, such as computer programming and matrices.

Applying the Meanings of Division in Your Math Class

The meanings of division already play a role in your math class, whether you are aware of them or not.

But knowing that there are five meanings can help you more easily make sense of the math you’re already teaching.

This is especially helpful in teaching word problems. Many educators are challenged by the fact that their students seem to “know the math,” but struggle to solve word problems. 

If you’ve faced this problem, you may have tried to teach your students “key words” to help them figure out what the problem is asking them to do. I go into more detail on the problem with key word strategies in my article on The Polya Process, but suffice it to say, key words are ineffective and counterproductive.

But once students know that there are only five types of division problems, they can categorize each word problem by the type of division being described. They will also begin to recognize the difference between partitive and quotative division, even if they don’t learn those terms.

For more on teaching division conceptually, explore our online store or register for one of our upcoming virtual workshops. 

Our resources are designed to make it easy for you to enrich your existing curriculum, and give your students opportunities to engage in hands-on, creative problem solving.

And our workshops walk you through the process of teaching problem-based math, such as visual modeling, strategic problem-solving, and more. All of our math workshops are offered for both elementary and middle grades.

If you just want to stay in the loop, sign up for our free Educator’s Newsletter. You’ll be the first to know when we publish a new post or launch a new offering. You’ll also receive special offers and discounts so you can save while growing in your teaching practice.

GET THE FREE NEWSLETTER

About the Author

Jeff Lisciandrello is the founder of Room to Discover and an education consultant specializing in student-centered learning. His 3-Bridges Design for Learning helps schools explore innovative practices within traditional settings. He enjoys helping educators embrace inquiry-based and personalized approaches to instruction. You can connect with him via Twitter @EdTechJeff