Do Math Standards Need to Be So Complicated?

Love them or hate them, math standards define how we teach math in today’s schools. While they may be necessary, many educators worry that standards can prevent us from teaching our students in an authentic, meaningful way.

Imagine your 5th grade students don’t understand the concept behind fractions. To top it off, they’re not strong with multiplying whole numbers. But the standards say they should learn to multiply fractions.

So rather than focusing on the concepts they need, we ‘teach the standards.’ And since our students lack the conceptual foundations, they struggle with grade level content. Ultimately, we’re forced to rely on tricks and algorithms to prepare them for the test.

Even when our students are on grade level, standards can prevent us from exploring the richness of mathematics. Schools that adhere too strictly to standards aren’t able to explore concepts in depth, or teach real-world applications.

Now imagine the flip side. What would it be like to teach math without any standards? A 1st grader in one school might learn about fractions, while another school might not touch fractions until 5th grade. What happens when students change schools? 

Two 6th teachers in the same school might cover different content. How is the poor 7th grade teacher to know where they left off?

Our current obsession with standards is actually a reaction to the chaos of unstandardized schools. Throughout the 1980’s and 1990’s, schools across the country taught different topics in different sequences. 

In part, standardization was an equity issue. Students from low-income urban and rural districts received less rigorous instruction and assessments than their wealthy suburban counterparts.

But Do Math Standards Need to be So Complicated?

Wherever you stand on standards, it’s hard to deny that math standards are complicated. I’d argue that they’re too complicated.

Here is a 2nd grade math standard, 2.OA.C.3, as found on AchievetheCore.org

The standard has two parts. The first is pretty straightforward – identify even numbers below 20. But the 2nd half asks students to “write an equation representing an even number as the sum of two equal addends.”

My first thought upon reading this is, “Does this really matter?” Of all the math that students need to be successful in school and life, how does this fit in? 

Sure, the question is a bit unfair. Many things that students need to know are foundational. You might not need manipulatives or visual models to be successful in life and math, yet they play a critical role in the development of numeracy.

Unpacking the Math Standards

When we unpack this standard, we can find a number of important concepts.

Students are asked to “write an equation.” The ability to write an equation is a valuable skill in and of itself. The meaning of equality is a critical concept for students to master in the early grades. Many students arrive in middle school thinking the equal sign means “the answer goes here.” Such misconceptions create incredible hurdles for students attempting to think algebraically.

Another skill embedded in the standard is representing even numbers as “the sum of two equal addends.” This specific skill doesn’t rise to the level of ‘understanding equality.’ But it does indicate are thinking deeply and flexibly about the underlying math. 

By 2nd grade, students have learned to count numbers. They’ve also learned to extend counting to the idea of addition. But seeing 10 as an even number because it’s equal to 5+5 will lead to expressions like ‘5 x 2,’ and ‘10 ÷ 2.’

So looking closely, we can see the value in this standard. But the question remains: “Is this the best way to describe what students need to know?” 

That’s a clear “no,” in my opinion.

If the goal is to help students understand equality, or connect addition to multiplication, why not just say so? 

Repacking the Math Standards

I think the designers of the standards wanted to do more than just write standards. They wanted to define how the standards would be taught. And that’s a mistake.

Standards should be milestones, or guideposts. Educators could look at the big ideas and figure out how to teach them. Maybe they use a textbook. Maybe they use an online platform. Or create their own curriculum from scratch.

I suspect that the standards weren’t written for educators. They were written for textbook publishers. By taking a granular approach, it allows publishers to easily translate standards into lessons.

In a way, this runs counter to the purpose of the common core. The standards were designed to move away from “mile wide, inch deep coverage.” They were designed to help students think deeply and meaningfully about math. 

In order to do so, we need to focus on big ideas and connections. And that requires a few changes to how we think about standards.

For one, standards need to be expressed in “teacher-friendly” terms. At the elementary level, this means acknowledging that most teachers teach multiple subjects. Few elementary teachers were math majors. 

And that’s not a bad thing. Should it really require a math specialization to understand what an 8-year old learns in math class?

We should also think carefully about teaching math as disconnected ideas. Each grade contains dozens of standards. But in reality, the important ideas from each grade level could be summarized in a few sentences. 

Phrasing standards in big picture terms serves all stakeholders. Students can understand what will be expected of them. Teachers become less reliant on textbooks. And parents won’t feel anxious or confused by what their children are being taught.

Standard = Concept x Representation

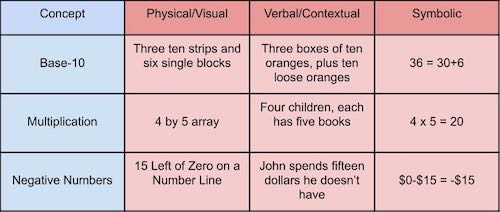
The good news is that math standards can be simplified with a simple formula: Standard = Concept x Representation.

Part of the reason standards seem so complicated is because they combine concepts and representations. While there are only a few of each, the combinations add up quickly.

Think of each concept as an ingredient. And each representation is a type of baked good. Imagine how many types of cookies, muffins, and scones you could make with chocolate chips, walnuts, and raisins.

With just chocolate chips, you would have three options.  Add walnuts, and suddenly you have six more possibilities. Introducing raisins expands your options to 21!

Now if you were learning to bake, you’d learn how to make cookies, muffins, and scones. And you’d learn about the possible ingredients. You wouldn’t learn how to make chocolate walnut scones one day, and chocolate raisin scones the next. 

But that’s exactly what we do with our math standards! Rather than introducing the big ideas and showing students how they’re connected, we cover every last permutation in granular detail. 

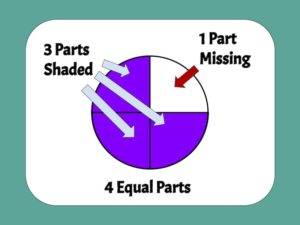
Here’s an example: 

 

If we can identify the ‘ingredients’ to each grade level standard, the content becomes much more manageable. Teachers and students better understand what they have in store. 

And we can teach the content much more efficiently. We would use less class time, and students would come away with a deeper understanding – which would also improve retention from one grade to the next.

Math Concepts: The ‘Big Three’ 

Surprisingly, there aren’t many actual ‘math concepts’ that students need to master at each grade level. In fact, all the math concepts we teach in school can be grouped into three categories:

• Numbers: The idea that numbers can count objects or measure spaces. Over the years the types of numbers become increasingly complex: from counting numbers to Base-10, fractions, negatives, and variables
• Operations: Operations are actually shortcuts to counting. Whether we’re counting up (addition) or counting down (subtraction). Whether we’re repeating addition (multiplication) or repeating subtraction (multiplication). Even exponents and square roots are extensions of multiplication. 
• Relationships: This category is a bit more nuanced. While an operation describes an action we perform on a single number, relationships involve comparing or linking two or more quantities. This includes concepts like equality, ratio, and functions.

These three categories are interrelated. For example, a fraction is both a number and an operation. And an equation is a relationship that contains numbers and operations.

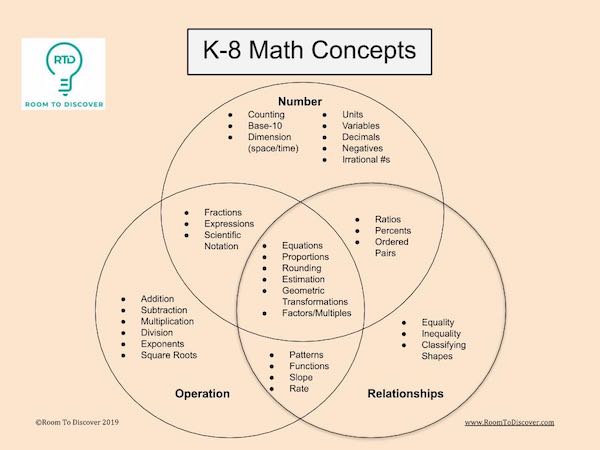
There is certainly room for debate about how to categorize the concepts. But regardless of how you group them, it helps to recognize that the goal of each year is to help students deepen their understanding of number, operations, and associations.

The Five Representations

The other half of our math standards equation is the Five Representations.

These five representations are all ways to represent the same mathematical idea. 

Representations are at the heart of conceptual understanding. So a student who truly understands fraction addition should be able to solve using an algorithm. But they should also be able to represent the operation with a visual or physical model. They should be able to explain what is happening, or apply fraction addition to a real world situation.

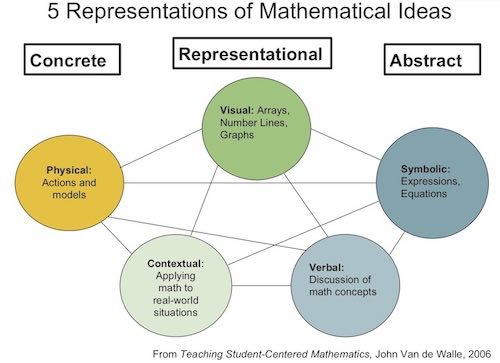
Traditional math classes focus squarely on symbolic representations. This includes our number symbols, operation symbols, and equal signs. 

Some still think of symbolic representations as “real math,” as if the other representations are something other than math.

The common core standards played a key role in spreading awareness that not all math is symbolic. The representations are now woven into our math standards. This enables us to go deeper in our math instruction, but it can also make standards more confusing.

Dividing Your Math Standards

I think it’s time to make our math standards more accessible. And the simplest way to do that is to divide out the concepts from the representations.

As we introduce each math concept, we can teach students to translate the new concept into each of the five representations. I use graphic organizers to scaffold this way of thinking.

But to do this effectively, we can’t rely on our textbooks. We need to look at our standards and identify which parts are concepts, and which are representations.

Dividing a 2nd Grade Math Standard

Standard: CCSS.MATH.CONTENT.2.OA.A.1 Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem
Concepts	Representations
Base-10 up to two digits Multi-step problem-solving Meaning of addition and subtraction Number as variable	Scale models Symbols (expressions, equations, variables) Real world (word problems)

In this standard, we are asking students to demonstrate mastery of adding and subtracting within 100. This requires that they understand addition and subtraction, and to apply base-10 understanding to operate with two-digit numbers. We also introduce variables, asking them to work with “unknowns in all positions.” Finally, they should be able to apply these competencies to multi-step problems. These are the math concepts from this standard.

But the standard also asks students to use multiple representations. So they should demonstrate base-10 understanding with models, with symbols, and in context. The same could be said for the other math competencies.

So, instead of a rambling standard that confuses concepts and representations, I prefer presenting the underlying competencies in a table as concepts and representations.

Dividing a 7th Grade Math Standard

Standard: CCSS.MATH.CONTENT.7.RP.A.2.A Decide whether two quantities are in a proportional relationship, e.g., by testing for equivalent ratios in a table or graphing on a coordinate plane and observing whether the graph is a straight line through the origin.
Concepts	Representations
Multiplicative comparison Ratio reasoning Proportional reasoning Functional reasoning (ordered pairs)	Symbolic (“quantities”) Scale models (coordinate plane) Tables (visual/symbolic)

This standard illustrates a granular approach, as we are asking students to test for proportionality. But it doesn’t address the concept of proportionality.

That concept is addressed, but in the ‘parent’ standard, 7.RP.A.2.

That standard contains 4 sub-standards, A through D. Each asks students to find a different way to test for proportionality or apply proportions to real world situations. For example, 7.RP.A.2.D asks students to ‘explain what a point on a graph means in terms of a situation.’

And while these are all worthwhile aspects of proficiency, they leave out many of the ways we could combine proportional reasoning with the five representations.

And presenting each aspect as a separate skill confuses teachers and students. I’ve seen many classes where students ‘test for equivalent ratios in a table,’ but don’t understand that a coordinate plane graph is just another way to represent that same relationship.

When students learn these skills in isolation, they tend to struggle most with word problems, the “real world” representation.

On the other hand, when students represent proportional relationships using a multiple representations organizer, they can more easily see the big picture.

So while breaking competencies into discrete skills can help us to assess student mastery, it is rarely the best way to actual teach the concepts. This is why education leaders warn against “teaching to the test.”

Simplify Your Approach to Math Standards

Organizing your math curriculum around standards and representations has enormous benefits. You’ll cover more content in less time, and your students will develop deeper conceptual understanding.

But it can be challenging to take this approach with a traditional textbook. Their units and pacing guides are designed for the granular approach.

If you’re ready to rethink your approach to content coverage, but don’t want to go it alone, we’re here to help. Our instructional coaches are experienced experts in curriculum design, lesson planning, and classroom best practices.

We’ll help you create unit plans and pacing guides that match your teaching style and your students’ needs. And we can support you in implementing these lessons, as well as assessing student work.

Contact us today to schedule a free consultation.

SCHEDULE MY CONSULTATION

About the Author

Jeff Lisciandrello is the founder of Room to Discover and an education consultant specializing in student-centered learning. His 3-Bridges Design for Learning helps schools explore innovative practices within traditional settings. He enjoys helping educators embrace inquiry-based and personalized approaches to instruction. You can connect with him via Twitter @EdTechJeff