How to Teach Fractions: 4 Strategies for Student Success
Knowing how to teach fractions can make all the difference for student mastery. Follow these tips to build your students’ conceptual understanding.

When I first learned about the Five Meanings of Multiplication, I was irrationally exuberant. Up until then, I’d always thought of multiplication as something you do.
I’d never really considered that there was a meaning behind multiplication. I started to wonder: who invented multiplication? Was it really even invented, or just discovered?
The fact that there could be exactly five seemed impossibly perfect. If someone did invent multiplication, did they plan for it to be used five different ways? It seems more likely that the five applications were gradually discovered over time, but we’ll probably never know.
Just to clarify, when I talk about the meanings of multiplication, I’m not talking about the traditional algorithm vs the lattice method. There’s no limit to the number of ways we can calculate multiplication. The meanings of multiplication are the reasons why we multiply.
For our students to be successful, they need to understand what the operations mean, and how each can be used in the world outside the classroom. Yet in my conversations with other math educators, many tell me they’ve never even heard of the five meanings of multiplication.
This is why I’ve decided to write this post. Most of what I know about the topic comes from Math Matters, by Suzanne Chapin and Art Johnson. Their ideas on cultivating a deeper understanding of multiplication is so important, I believe every math teacher would benefit from a concise explanation. But if you’d like to go deeper than what’s contained in this post, I recommend picking up a copy.
Many students memorize their times tables and “stack” to solve, but still don’t understand the meaning behind the numbers and operations. When students struggle with word problems and mathematical writing, it’s often a sign they lack conceptual understanding. Download your FREE WORD PROBLEM ORGANIZER, and help your students begin seeing the meaning behind the math.
To better understand the meanings of multiplication, I like to imagine a time before multiplication existed. You’d have to go back at least to the ancient Babylonians, who are said to have invented times tables over 4,000 years ago.
But there’s also evidence that someone in sub-Saharan Africa actually discovered multiplication over 20,000 years ago! A tool called the Ishango Bone, found on the border of present-day Uganda and the Congo, can be used for a variety of mathematical purposes, including multiplication calculations, and even as a calendar.
So we may never know who invented multiplication. So let’s just picture a woman counting boxes of dates in a dimly lit room with clay walls. Each wooden box holds 24 dates. The boxes are stacked 5 high, 4 across and 6 deep.
To find out how many dates she has, this poor woman has to add 24, plus 24, plus 24, plus 24, on and on and on. But then she starts to notice a pattern. Then, suddenly, she has a Eureeka moment: “Wait a minute! Each box has the same number of dates. What if there was a shortcut for counting a large number of equal groups?” And multiplication was born.
Over time, the same strategy would be used to find area, volume, combinations, and more. And eventually, Chapin and Johnson were able to identify five unique purposes for multiplication. (It should be noted that each meaning of multiplication also applies to division, its inverse)
Equal groups is how we typically think of multiplying. It’s the classic problem of counting boxes of dates. Students tend to have the easiest time recognizing these problems in context.

Dividing by equal groups is trickier. Most students see division as ‘splitting into a set number of groups.’ For example, if I have 8 cookies to divide among four friends, how many does each friend get? This is called partitive division.
But division can also mean splitting into ‘groups of a set size.’ So if I divide those same 8 cookies into groups of 2, how many friends can I share with? This is quotative division (or repeated subtraction).
To illustrate how important the difference is, I use the example of a shoe factory manager leaving for the day. She points to a pile of 100 shoes, telling her employee to ‘divide them by two and put into boxes.’ The next day, she’s shocked to find 50 shoes shoved into one box and 50 into another.
For more on the partitive and quotative division, check out my post on Teaching Division for Conceptual Understanding.
While I love all the meanings of multiplication, if I had to pick one, I’d pick the rectangular array.
Rectangular arrays lend themselves beautifully to visual models, including both arrays and area models.

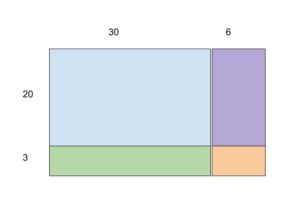
An Array and an Area Model, both Examples of the Rectangular Array meaning of multiplication
A simple array is a set of objects organized into rows and columns. It provides a foundation to help students understand area and area models, which are measurements of two-dimensional space.
Many of our students only understand number as quantity, or distinct objects. Arrays and area models can help them connect this idea that they already know to the idea of number as a measure of space.
When we teach area, we usually teach students that area is a formula: “l x w,” “½ b x h,” or even “????r².”
But area is so much more than that. It’s an entirely different meaning of multiplication, and of number. I teach students that we live in a 3-dimensional world, and we can measure in all three-dimensions.
Length is a measure of 1 dimension, area is a measurement of two, and volume is a measurement in three dimensions. Theoretical mathematicians keep going into the 4th dimension and beyond.
Today, we tend to think of measures of space (geometry) as less important than quantities. The geometry unit is always at the back of the textbook, and we rarely see geometry standards in the “focus standards” for any grade level. But to the ancient Greeks, it was the complete opposite.
By using rectangular arrays, we can help our students go beyond seeing area as a formula. This can help them to stop confusing area and perimeter. They’ll also have an easier time seeing volume as an extension of area, rather than as a completely new concept.
Multiplicative comparison is another area that many students find difficult. These are situations where one thing is x many times as big as something else. I may be twice as old as Jermaine’s sister, or have one third as many cookies as Sonja.
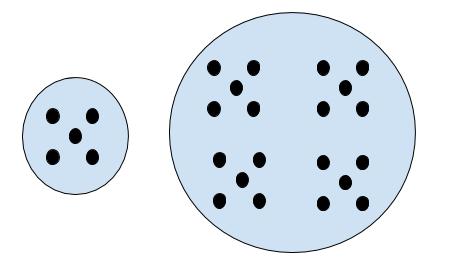
One reason these problems are challenging is because students tend to think of operations as something we ‘do to’ a number. So when I multiply 5 apples by 7, I’m adding a bunch of extra apples. But with multiplicative comparison, I’m describing differences that already exist.
Another reason for difficulty is that students confuse these problems with additive comparison. Many will simply add four when asked to find ‘four times as many.’ Other students may not be strong enough with additive comparison (they understand addition as combining, but not comparing).
Students need an understanding of multiplicative comparison to handle middle school standards, such as ratios and geometric transformations.
When teaching multiplicative comparison, provide students examples of additive comparison and multiplicative comparison. This ensures that they understand both concepts, and that they can tell the difference between them.
Rates are not introduced until middle school, but the foundations are laid much earlier. Before students are introduced to multiplication, they are taught skip counting and repeated addition. This idea of repeatedly adding the same quantity, is essentially the same concept behind rates.
Rates are similar to equal groups, except that equal groups are static, while rates involve a repeated process, typically over time. I could have 4 boxes of 24 dates, an equal groups problem. Or I could eat 24 dates an hour for 4 hours, making it a rate problem.
The difference is the “per hour,” which is actually an embedded division problem, or fraction:
4 hours x 24 dates/hour = 96 dates
As in most rate problems, the denominator of our rate is ‘1.’ (Making it a unit rate). We eat 24 dates for every 1 hour. Since we’re dividing by 1, most adults simply ignore the division.
But this can create confusion for students. The division is important, because it affects our units. It’s not correct to say “4 hours times 24 dates.” That would make our result “96 date-hours.”
Instead, the hours in the denominator of the rate cancel the hours in “4 hours,” giving us 96 regular dates.
Students may also be asked to find a rate. In this case, we take the total amount and divide by the period. If we knew that we ate 96 dates over 4 hours, our rate would be 96 dates per 4 hours. Or we could simplify to find the unit rate:
96 dates ÷ 4 hours = 24 dates/hour
Rates are crucial for much of later math, including functions, slope, and pretty much everything in calculus.
Cartesian products are the least common, least understood meaning of multiplication.
A Cartesian product is another way to describe combinations. These problems often include matching shirts and pants to make different outfits, or different ways to stack an ice cream cone.
To find a Cartesian product, pair each element from the first group with each element from the second group. This can be represented visually, in a table. The total number of possible pairings is your product.
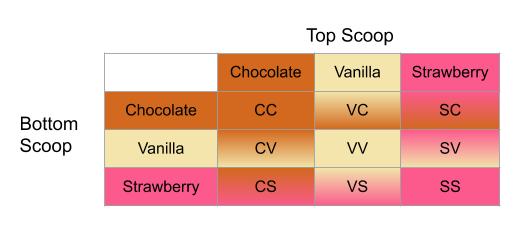
Multiplying to find combinations is a foundation for probability. In the above example, if you are randomly assigned a cone, the probability it has only one flavor is 3 out of 9, or ⅓.
The idea of matching values together also introduces ordered pairs, hence the name “Cartesian” product, as in Cartesian plane.
Cartesian products can be introduced through games and activities, such as dice and cards. I used to hold Roshambo tournaments (rock paper scissors) to teach about combinations and introduce game theory.
Learning the meanings of multiplication not only helps students develop deeper understanding, it also supports fluency with basic operations. When students can connect operations to relatable scenarios in their lives, they can more easily see how multiplication is a repetition of addition, an inverse of division, and so on.
This doesn’t take the place of times tables or algorithms. But it certainly reinforces them. It also helps students to make sense of word problems.
One way to help students understand the meanings of multiplication is to demonstrate them with visual models and manipulatives. As students become comfortable with these multiple meanings, they will begin to recognize them in the context.
In our online store, you can find interactive digital activities that support conceptual understanding of multiplication, and integrate easily into google classroom. For the elementary grades, you’ll find lessons for teaching arrays, area models, volume, and operations with fractions. Middle and high school students will benefit from our lessons on rates, percents, functions, and more.
Eventually, students should be able to apply their understanding of multiplication to abstract situations. One way to support this transference is with equation proofs. Equation proofs are a structured way to get students to go beyond solving equations to actually explain why equations are true, false, or “sometimes true.” Equation proofs can be done with or without variables, to reinforce students’ understanding of fractions, integers, exponents, and more.
For more strategies that increase student engagement and support conceptual understanding, sign up for our weekly Educator’s Newsletter. You’ll also get a free gift: our Problem-Solving Graphic Organizer, that helps students make sense of word problems, without relying on tricks and key words.

Jeff Lisciandrello is the founder of Room to Discover and an education consultant specializing in student-centered learning. His 3-Bridges Design for Learning helps schools explore innovative practices within traditional settings. He enjoys helping educators embrace inquiry-based and personalized approaches to instruction. You can connect with him via Twitter @EdTechJeff

Knowing how to teach fractions can make all the difference for student mastery. Follow these tips to build your students’ conceptual understanding.

Teaching word problems takes more than key words. The Polya Process helps your students think strategically and make sense of story problems.
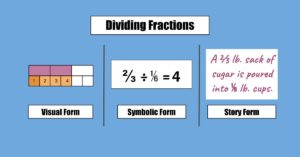
Learn visual models and other strategies for fraction division to help your students go beyond keep-change-flip and build conceptual understanding.