How to Teach Fractions: 4 Strategies for Student Success
Knowing how to teach fractions can make all the difference for student mastery. Follow these tips to build your students’ conceptual understanding.
What role do visual models play in the modern math classroom? Are they something that’s nice to have…if we have the time? Are they a distraction from the ‘real math’ that we should be teaching students? Or are they an essential ingredient in the development of conceptual understanding?
A clue to the value of visual models can be seen in the impact of Singapore Math. Beginning in the early 1980’s, Singapore, a single city South Asian nation, redesigned their math curriculum to emphasize the use of visual models and physical manipulatives.
By the 1990s, Singapore had emerged as an international juggernaut of math education. Standardized tests such as TIMMS (Trends in International Mathematics and Science Study) and PISA (Programme for International Student Assessment) consistently showed Singapore at the top. (They’ve recently fallen to #2, behind China).
The US, on the other hand, currently ranks 37th out of 78 tested nations. While we came in just ahead of countries like Belarus (38) and Kazakhstan (54), we placed well behind rivals like Russia (22nd) and China (1st).
A 2005 American Institute for Research study compared math instruction in Singapore and the US, finding that Singapore placed a greater emphasis on conceptual understanding. Later, the designers of Common Core Math Standards relied heavily on Singapore’s approach.
But now, many states are pulling back from Common Core; partly due to parent complaints, and partly due to flat test scores. You might ask, are visual models overrated?
No. The issues with Common Core are complex, and largely a result of poorly written textbooks and outdated approaches to professional development.
But the research is clear. A 2014 study found that students who use visual models were six times as likely to correctly solve word problems. And a 2012 study found that students with learning disabilities were less likely to use visual representations. But when they were explicitly taught to use them, their performance improved substantially.
Need a crash course on bringing visual models and manipulatives to your math classroom? Registration is now open for our online Elementary School and Middle School visual models workshops.
Halfway through my teaching career, I experienced the power of visual models first-hand, in my own classroom. I had just switched from teaching English to math. (Weird, I know).
Early in the year, my 5th graders took the diagnostic test at the beginning of the textbook. IT was meant to review what they’d learned in 4th grade, but they bombed it. The highest grade was around 40%.
I tried charging forward with Chapter 1. But they were completely lost. Fortunately, a colleague introduced me to Khan Academy, which was a lifesaver. It gave my students differentiated lessons and provided me with detailed insights into what each student needed.
I also noticed that Khan used a lot of visual models. In fact, I completed a lot of the lessons myself, just so I could learn about arrays, area models, and so on. I’d never learned these things growing up, so I needed to play the student before I could teach them.
The lessons involving visual models were really having an impact. And most of my students really enjoyed them. Soon, I began incorporating visual models into my own lessons We even did a visual models video project.
But some of my students resisted using visual models. Interestingly, most of the resistance came from my “advanced students.” The “struggling learners” were thriving. Arrays and number lines were helping them fill in gaps they had accumulated over years of procedural math.
The visual models were really leveling the playing field. Students who were convinced they were “no good at math,” began to thrive. And those who were great at memorizing times tables and ‘stacking’ were pushed, for the first time, to demonstrate conceptual understanding.
Visual models play an important role in conceptual math. Not only are they effective tools for developing conceptual understanding, but they are a great way to assess such understanding.

One reason is somewhat obvious. Visual models, when drawn to scale, make clear what numbers and operations mean. If you model ‘357’ with base-10 blocks, it’s clear that the 3 hundreds are much bigger than the 7 ones. And if you create a 4 x 8 array, it’s easy to see why 4 times 8 is 32.
But the vast majority of math class is spent in the symbolic realm. Students memorize times tables, perform operations by stacking, and divide fractions with ‘keep, change, flip.’ These procedures allow them to perform calculations without understanding the numbers they’re manipulating or the operations they’re performing.
This surface understanding is problematic for several reasons. For one, students don’t remember what they’ve learned. The brain is designed to weed out disconnected bits of information. In order for students to retain what they learn, they must connect it to something meaningful.
Another problem is application. Every math teacher knows the agony of the word problem. “They understood the math. But they just can’t do word problems.” The issue is not ‘literacy.’ The issue is that students can only apply math to real-world scenarios when they actually understand it.
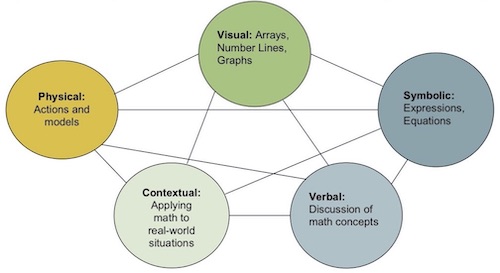
John Van de Walle addressed The Five Representations of Mathematical Ideas in his seminal book, Teaching Student-Centered Mathematics. We can take any mathematical idea and represent it physically, visually, symbolically, verbally, or contextually. He explains that when students can translate from one representation to another, “there is a better chance of a concept being formed correctly and integrated into a rich web of ideas.”
To get the most out of visual models, it’s important not to think of them as ‘one more thing we have to cover.’ Models are a tool for helping students understand the math you’re already teaching. Instead of worrying that you ‘need to teach times tables and arrays,’ use arrays to demonstrate the meaning of multiplication.
Unfortunately, it’s not always easy to figure out which models to use, or how to connect them with your grade level standards.
While the modern math standards in the US are a vast improvement over the pre-Common Core standards, they can sometimes be confusing. If you’ve spent any time reading the CC Standards, or your state, you’ve probably noticed that quite a few skills can be wrapped up in a single standard.
To break standards down into manageable pieces, I use a framework called 4-D Math. I started noticing that the concepts embedded in math standards could be organized into 4 main categories:
I realized that the standards were really just a long, complicated description of how these dimensions combined to form a mathematical concept. By separating them back into the 4-dimensions, I could easily understand individual standards, see connections between standards, and come up with conceptual approaches for teaching each standard, (including visual models).
For example, take a look at this 3rd grade standard from the Operations and Algebraic Reasoning domain:
I think this is a perfectly reasonable expectation for a 3rd grader. But there is a lot wrapped up in here. If, instead, we break it down into the 4-dimensions…
Imagine you had a student who was struggling with this standard. By breaking it down, we can assess each element independently.
A 4-D breakdown can also help us decide which visual models are the best fit for the standard we’re teaching.
What is a number?
The answer to this question is constantly changing as our students progress through their math journeys. And at every stage, visual models remain a powerful way to extend their understanding.
Students’ first exposure to math is through counting. Any uniform object or image can be useful, but counting discs are widely-used to teach number names and cardinality.
By first and second grades, students’ develop two critical numeracy concepts, Base-10 and ‘number-as-length.’
Ten Frames help students to organize counters into tens, and begin to appreciate the importance of ‘10’ in our number system. Then, they extend their understanding into larger numbers, counting by tens, and so on, through the use of Base-10 Blocks.
At this age, students are also exposed to the idea of measurement. Previously, numbers were understood to be an ordered list (1, 2, 3…) or a collection of objects (quantity). By measuring objects and introducing number lines, students begin to see length as a type of number.
In grades 3-5, students continue to develop their understanding of Base-10 and measurement. But what makes this period unique is the idea that a whole number can be broken into parts.
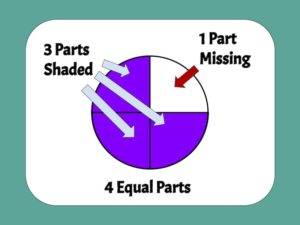
We begin by using Fraction Circles to introduce halves, thirds, and quarters. Then, we move to Rectangular Fraction Models to represent a wider range of denominators, as well as decimals.
Once we’ve established the concept of a decimal, we revisit Base-10 Blocks, this time to extend understanding of place value to smaller decimals, such as hundredths and thousandths. Finally, we connect fraction and decimal understanding to the concept of measurement by representing fractions and decimals on a number line.
In grades 6-8, the concept of a number becomes more abstract, with the introduction of negative numbers and variables.
A number line is usually the easiest introduction to negative numbers. As students should already be familiar with number lines, we simply extend them to the left of the zero. (Or below the zero in the case of vertical number lines).
And while students should have some exposure to variables in elementary, it’s not until middle school that they become central to the curriculum. Variables can be tough to represent visually, as we don’t know their exact size. But algebra tiles do a good job of making the abstract concept a bit more concrete.
Just as a surgeon performs operations on her patients, operations are actions that we perform on numbers.
There are a few critical understandings that students should develop around operations. One is the basic definition of an operation, described above. And as they learn each new operation, they should connect it conceptually to those they’ve learned. For example, teach subtraction as the opposite (or inverse) of addition, and multiplication as a repetition of addition.
Just as students’ understanding of number gradually becomes more sophisticated, so does their understanding of operations. But while new types of numbers are introduced almost every year, the four basic operations remain the main focus after grade 3. The learning consists of applying these operations to the new types of numbers students encounter.
Visual models play an important role in the introduction of operations, their interconnectedness, and their application to different number types.
When modeling operations, it’s important to show the action being performed, not just the result. For example, a model showing 3/4 is not the same as a model of 1/2 plus 1/4. When modeling operations, be sure to make clear the starting value, the action performed, and the result. This can be done by drawing the three stages, using color coding, arrows, and so on.
Students in the early grades are first exposed to addition and subtraction, as an extension of counting and cardinality. They can count to 5, then count three more, or combine two groups of apples and count the total. Eventually, they will learn four meanings of addition: counting on, combining, extending (measurements), and comparing. They will also learn that each of these performed in reverse is subtraction.
As addition and subtraction are so closely related to counting, the same visual models used to introduce numbers are also used for these operations. Counters can be used alone or with part-part-whole organizers and ten frames. Number lines are a good tool for addition, but especially useful for subtraction, as students can learn to think of subtraction as the distance (difference) between two numbers. This leads to ‘counting up’ as a mental math strategy for subtraction.
Operations become significantly more complex in grade 3, as students encounter multiplication and division. Eventually, they will learn all Five Meanings of Multiplication (and division), but we typically start with repeated addition or equal groups.
Then, they create arrays, multiplying by arranging objects into rows and columns. This prepares them for area: rows and columns become lengths and widths, and counting objects becomes the measurement of a two-dimensional space. Area models can be used to reinforce the concept of area (grade 3), to multiply multi-digit numbers (grades 3-4), and to multiplying fractions (grades 4-5).
By grade 5, students extend their understanding of 2-D measurement (area) to 3-D measurement (volume), which can be modeled with unit cubes and 3-dimensional arrays.
Since division is the opposite (inverse) of multiplication, each of these modeling strategies can also be used for division. When modeling multiplication, we give students two factors, and they find the product. To model division, we provide the product (dividend) and one factor (divisor), and they find the other factor (quotient).
By middle school, students have learned all 4 operations with whole numbers, fractions, and decimals, with one exception: dividing a fraction by a fraction. Fraction division can be represented with bar models, which will also be useful for a number of other middle school concepts.
For the most part, though, the focus will be on applying the four operations to negative numbers and variables. As the math concepts get more abstract, it takes some creativity to represent them with visual and physical models. Creating zero pairs with integer discs is a clever way to represent addition and subtraction of integers. And number lines are also effective for adding and subtracting integers and rational numbers.
To multiply integers, I create arrays with integer discs. First, I model one factor (yellow for positive, red for negative). If the second factor is negative, I’ll flip all the chips over. But for this type of modeling to be effective, students need to have a solid foundation in modeling concrete numbers and operations.
Algebra Tiles are helpful for modeling operations with variables, especially when combining like terms.
Students are also exposed to two new operations in middle school: exponents and roots. The trick to visualizing exponents is modeling repeated multiplication. A square can simply be an array or actual square, and cubes can be shown with unit cubes or 3-dimensional arrays. To show 25, start with a 2 x 2 array (22), then stack another on top (23), and keep iterating until you’ve doubled 5 times (25).
Other exponents become more complex, so again, you’ll need to get creative. For negative exponents, you could work in two stages: first, model without the negative to find the denominator, then create a simple fraction model.
For simple square roots (fractional exponents), count out the radicand in discs. Then, try to create a square array. The number of rows or columns will be the root. You can also use this Desmos activity for modeling square roots.
One aspect of math instruction that is often overlooked is the importance of connections. It’s easy to see the importance of numbers in math, as well as the operations we perform on those numbers. But most math in the real world involves numbers interacting with each other.
The clearest example is the concept of equality. Students in first grade are supposed to learn the concept of equality as balance. Yet many students make it to middle school and beyond thinking that the equal sign means “the answer goes here.” The National Council of Teachers of Mathematics (NCTM) free online balance tool has a that can help students visualize the meaning of equality. This idea also extends to the concept of inequality – just as equality can be visualized with a balanced scale, inequality can be shown as an unbalanced scale.
Another important progression is that of patterns and functions. Patterns are one of the first math concepts students encounter – often before they are even exposed to numbers. Eventually, the pattern concept evolves to the idea of a function: a connection between an independent and dependent variable.
The coordinate plane (x-y graph) is the current standard for representing functions visually. But though it is a representational (scale) model, many students work in the coordinate plane without actually understanding the meaning of what they are showing.
To develop conceptual their conceptual understanding, students should learn to represent functions in multiple forms: visually, symbolically, contextually, and so on. Growing Shapes are particularly useful for modeling the progression from pattern to function.
Proportions are another important connection, which also include aspects of operations (multiplicative comparison). Proportional reasoning plays a role in many middle school standards, including unit conversions, percentages, and rates. Proportions can be visualized using bar models, double number lines, and the coordinate plane.
Visual models are one of the most powerful tools for increase student engagement and achievement. In this post, I’ve tried to give you the foundations you’ll need to make visual models a staple of your math classroom.
Of course, there’s only so much you can learn from a single blog post. So if you found this helpful, you’ll want to register for one of our upcoming workshops. In these hands-on, interactive workshops, you’ll collaborate with fellow teachers and come away with the strategies and resources you need to bring the learning back to your classroom.
You’ll also find visual models activities for almost any math standard in our online store.
Finally, don’t forget to sign up for our Educator’s Newsletter. You’ll receive our latest posts in your inbox each week, and you’ll be the first to know about new products, discounts, and special events.
 Jeff Lisciandrello is the founder of Room to Discover and an education consultant specializing in student-centered learning. His 3-Bridges Design for Learning helps schools explore innovative practices within traditional settings. He enjoys helping educators embrace inquiry-based and personalized approaches to instruction. You can connect with him via Twitter @EdTechJeff
Jeff Lisciandrello is the founder of Room to Discover and an education consultant specializing in student-centered learning. His 3-Bridges Design for Learning helps schools explore innovative practices within traditional settings. He enjoys helping educators embrace inquiry-based and personalized approaches to instruction. You can connect with him via Twitter @EdTechJeff

Knowing how to teach fractions can make all the difference for student mastery. Follow these tips to build your students’ conceptual understanding.

Many educators are starting to recognize the problem with homework. And while homework is almost universal, there is little evidence that it actually works.

Essential reading for every math teacher! The meanings of multiplication support student engagement, conceptual understanding, and success with word problems.