
Do You Know the Five Meanings of Multiplication?
Essential reading for every math teacher! The meanings of multiplication support student engagement, conceptual understanding, and success with word problems.
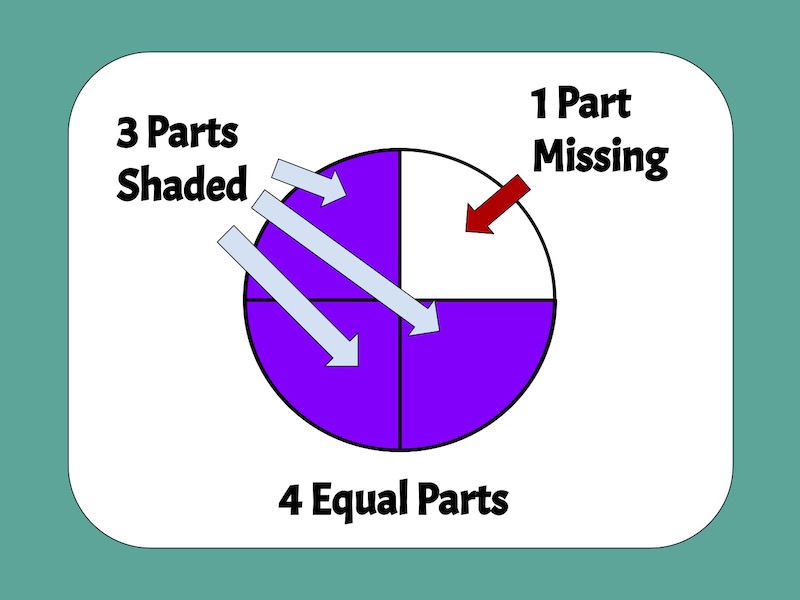
What is it about fractions? It seems like every math teacher wants to know how to teach fractions more effectively. And few topics create more anxiety and frustration for teachers, students, and even parents.
Most standards and textbooks introduce fractions in 3rd grade. But many students still struggle with them throughout middle and high school.
What can you do when younger students get confused? And how can you help older students learn the basics, without falling behind on grade level content?
The good news is that anyone can learn how to teach fractions. All it takes is identifying the most common misconceptions. And using a few simple strategies that can give your students a solid foundation in fraction concepts.
Looking for a visual, interactive, and conceptual approach to teaching fractions? Something that doesn’t require hours of planning time? Get your copy of our Fraction Essentials Bundle to help make fractions make sense.
Fractions are confusing because they don’t look or act like most of the numbers we’re used to.
The idea that there are numbers between 0 and 1 is tough for students. It challenges their understanding of what a number is.
They first define numbers as counting numbers. They can point to a group of objects and count up one-by-one. Next, they learn base-10, which allows them to organize numbers into tens, so they can count large quantities.
Then fractions come along and throw a wrench into the works. It’s no longer about counting, or making tens. Suddenly, a whole can be split into halves, fifths, or even thirty-sevenths.
On top of the conceptual challenges, fractions look and act a bit odd. Are they one number, or two? Why does a bigger denominator make a fraction smaller? Why do I flip the second fraction to divide?
Given these challenges, it can be tempting to avoid fractions completely. But it’s important that teachers at all grade levels understand how to teach fractions. Especially when students arrive in their class without the foundations.
Students who don’t learn the fundamentals continue to struggle throughout their math education. Whenever they come across topics like ratios, slope, and algebraic expressions, the old problems resurface.
Besides their abundance in schools, fractions surround us in the real world.
When we’re trying to eat healthy, we may only go for half of a cookie. Our most popular coin (in the US) is worth 1/4 of a dollar.
US customary units are designed for fractions. Gallons are divided into four “quarts,” and feet are made up of 12 inches.
While many people prefer the simplicity of the metric system’s adherence to groups of ten, there are benefits to standard units. Groups of ten can only be divided by 2 or 5. But 12 can be split evenly into groups of 2, 3, 4, or 6. This flexibility comes in handy in carpentry, cooking, and many other areas.
Their unique ability to divide a whole into any number of pieces you wish is what makes fractions so special. But it’s also what can make them challenging. Those who understand fractions may not even notice them. But to the fractionally-impaired, they can be a constant nuisance.
At one point, the A&W fast food chain introduced a ⅓ pound burger to compete with the quarter pounder. But they discontinued it when they realized customers thought ⅓ pound was less than ¼ pound.
Many students are eager to put fractions in the rear view mirror after grade school. And most middle and high school teachers are just as happy to avoid the topic. But understanding fractions is essential to success in higher math.
I once tutored an 8th grade student who was having trouble in Algebra I. We reviewed the tests she had failed, and I noticed that all her mistakes had one thing in common: fractions.
I asked a few questions, and realized she had no idea what the numerator and denominator meant. She had learned tricks to add, subtract, multiply, and divide fractions. But she had never learned (or had forgotten) the underlying concepts. In her mind, it was all about randomly moving numbers around the page.
This meant she didn’t understand what it meant for a line to have a slope of ¾. She couldn’t simplify rational expressions with inverse operations — because she didn’t connect fractions to division. And she didn’t understand how ratios, rates, and percentages worked.
She could apply algorithms if the problem was straightforward. But she was lost when attempting word problems or any problem with multiple steps.
It might seem that knowing how to teach fractions requires years of experience teaching math. Or that you need fancy software and expensive curriculum.
The truth is that understanding fractions is pretty simple. It all comes down to three concepts: numerators, denominators, and fraction notation.
Of course, there is more to know about fractions than this. But these concepts provide the foundation. Once students have mastered these basics, they realize that fractions aren’t magic. They’re just numbers.
Then, they can apply everything they already know about numbers and operations to working with fractions.
Knowing how to teach fractions means targeting the first place students get stuck: the denominator.
Put yourself in their place. When they first meet fractions, our students already use numbers to count, measure, and compare. So it just doesn’t make sense that 37/100 could be smaller than ⅔. Or that ⅓ is bigger than 1/10.
A denominator is unlike any number they’ve learned before. A denominator isn’t for counting “what we have,” but for telling us “what we’re counting.”
Imagine a colleague tells you, “I left three in your room.” That doesn’t mean much unless they answer the question, “three of what?” Three candy bars in your room is great. Three lions – oh no!
That’s the importance of the denominator. The numerator tells us how many pieces we have. But it doesn’t mean much until we know how big each piece is.
1st and 2nd grade geometry standards introduce students to the concept of cutting a whole into equal parts. Standard 1.G.A.3 has students “Partition circles and rectangles into two and four equal shares” and describe the parts as halves, fourths, and quarters. In 2nd grade, 2.G.A.2-3 extend this understanding to include thirds and rectangles.
Neither of these are focus standards — common core describes them as “additional standards,” meaning they are less important at that grade level. As a result, many 3rd graders are introduced to fraction notation without the right foundations.
Once students understand denominators, understanding the numerator is a breeze. Numerators work just like any other counting numbers.
In 3rd grade, the domain, Number as Fractions (NF) appears in the standards. And it’s assumed that students already understand the essence of fractions – cutting a whole into equal parts.
The first standard in this domain, 3.NF.A.1, starts with “unit fractions.” Unit fractions are those with a numerator of one, such as ½, ⅓, ¼. It then goes on to address fractions with numerators other than 1, such as ⅔, ⅗ and so on.
The final step in how to teach fractions is the notation. This is the idea that a fraction is a single number, made up of a numerator, a denominator, and a line in-between them.
When students get to third grade, they are introduced to fraction notation, often without the foundational concepts. The standards and textbooks assume they’ve already mastered partitioning in 1st and 2nd grades.
And by 3rd grade, fractions are a focus standard. But 3rd grade teachers don’t usually have the 1st and 2nd grade teaching materials. And since the foundations for fractions come from the Geometry domain, many teachers don’t realize that fractions are connected to the geometry standards.
(That’s why the coherence map from Achieve the Core is such a useful tool. When you map a standard, it shows you how each standard relates to prior and following grade levels).
This disconnect explains why so many students struggle to understand fractions year after year, to understand fractions.
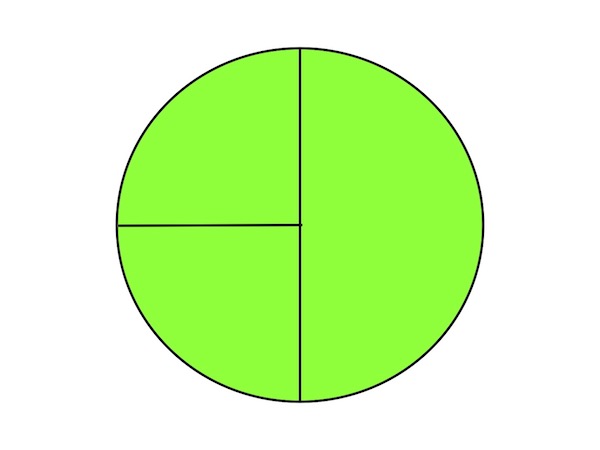
Yes, they may forget the terms numerator and denominator. But the vocabulary isn’t the real problem. When students keep making the same mistakes comparing fractions, simplifying them, or performing operations, check for concepts.You’d be amazed to learn how many middle school students will incorrectly cut a circle into three equal parts.
So make sure your students understand the denominator cuts a whole into equal parts. And a numerator counts those parts.
Then, it’s simply a matter of writing one on top of the other, with a line in the middle.
I pretty much relied on trial and error as I learned how to teach fractions. Eventually, I figured out what works. And more importantly, what doesn’t work.
Like most teachers, I started by teaching the way I was taught: by focusing on algorithms and “tricks.” Find a common denominator. Multiply across. Keep change flip.
But at the end of the day, I was just teaching students to get answers. Answer-getting is what non-mathematicians think math is for. Mathematicians know that math is a language. A thing of beauty. A lens that gives us a deeper understanding of the world around us.
And keep-change-flip….that’s not any of those things.
Sure, tricks have their place. Once students understand the concepts, they can understand how the tricks work. That allows them to apply the tricks appropriately.
But when we skip the conceptual understanding, tricks become counterproductive. Students learn that math is an arbitrary set of rules. Something that only “math people” understand.
Students who only know the tricks don’t check their answers. They don’t show their work. They make random guesses. And they apply the wrong trick at the wrong time. And when they could really use the tricks to solve a word problem or simplify an expression…they don’t even realize it.
So if you just want your students to get answers. And to forget most of what they learn a week later, then stick to tricks.
But if you want to know how to teach fractions the right way, try these classroom-tested strategies.
Like any math standard, fractions don’t exist in isolation. Understanding fractions helps with any number of advanced math concepts. But it requires certain foundations in numbers and operations. Before introducing fractions, conduct formative assessments of these two concepts.
First is the meaning of division. And since division is the undoing of multiplication, they should understand the meanings of multiplication as well.
They should be able to show you how 6 divided by 3 can be represented two ways. As 6 objects split into 3 groups, with two objects in each. Or dividing six objects into groups of 3.
Once they understand how to split groups of objects into equal-sized groups, the next step is to split a whole into equal parts. If students understand the meaning of division, and can apply it to cutting shapes into equal parts, they should be ready for numerators and denominators.
Nothing will short-circuit conceptual learning faster than teaching algorithms too early.
Sometimes, we don’t have any choice about how to teach fractions. You can send students home with a great conceptual activity for dividing fractions, only to have a parent teach them to keep-change-flip.
But too often, students are learning these tricks at school. And before they develop conceptual foundations.
I heard a great saying recently: “Shortcuts save locals time, and get out-of-towners lost.”
Nowhere is this truer than in math class. Once students have the concepts, they can learn how algorithms work and apply tricks effectively.
But teach them too soon, and students get lost. And once they’re fixated on answer-getting, it’s hard to convince them to take the “scenic route.”
Visual models and manipulatives are one of the most effective ways to teach any math concept.
And they act as great assessments as well. Ask your students to draw visual models. You’ll see why one of my favorite maxims of math class is, “If you can’t draw it, you don’t get it.”
Visual models are especially effective for teaching fractions. Since fractions work differently from more familiar numbers, visual and physical models clear up many misconceptions.
I use google slides with digital manipulatives to introduce fraction basics, multiplying fractions, and any number of fraction concepts.
I also cover fraction visual models in-depth in both my elementary visual models workshop, and my middle school visual models workshops.
Visual models and manipulatives are probably the most effective way to introduce fraction concepts.
But once they are strong in the foundations, students should also learn how to use fractions in expressions and equations. This helps students think more flexibly about fractions and deepen their abstract thinking.
A fun way to introduce students to expressions and equations is through number sentence proofs. In this activity, students don’t just find answers. They determine whether an equation is true or false, and then prove it. Use this downloadable Google Slides activity to introduce fraction number proofs to your students.
You can also participate in an online workshop on designing and teaching number proofs, expressions and equations: Choose Expressions and Equations in Elementary or Expressions and Equations in Middle School.
I hope this post has given you some fresh ideas for how to teach fractions. And for understanding why students struggle with fractions.
There is a lot to consider, and it’s important not to get overwhelmed. Your students may be on the verge of mastering fractions. Or you may first need to back and review concepts from several grade levels.
Your job isn’t to ensure that all your students master fractions right away. If one idea from this article changes how you teach fractions, you’ve accomplished something.
If you’d like to bring interactive fractions lessons to your students right away, check out our Fraction Essentials Bundle. It includes everything you need (eBook, printable classroom activities, and interactive Google Slides) to make fractions make sense.
Get Your Copy of FRACTION ESSENTIALS
 Jeff Lisciandrello is the founder of Room to Discover and an education consultant specializing in student-centered learning. His 3-Bridges Design for Learning helps schools explore innovative practices within traditional settings. He enjoys helping educators embrace inquiry-based and personalized approaches to instruction. You can connect with him via Twitter @EdTechJeff
Jeff Lisciandrello is the founder of Room to Discover and an education consultant specializing in student-centered learning. His 3-Bridges Design for Learning helps schools explore innovative practices within traditional settings. He enjoys helping educators embrace inquiry-based and personalized approaches to instruction. You can connect with him via Twitter @EdTechJeff

Essential reading for every math teacher! The meanings of multiplication support student engagement, conceptual understanding, and success with word problems.

Teaching word problems takes more than key words. The Polya Process helps your students think strategically and make sense of story problems.
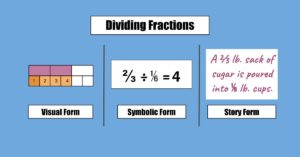
Learn visual models and other strategies for fraction division to help your students go beyond keep-change-flip and build conceptual understanding.