Teaching Fraction Division: A Visual and Conceptual Approach

Few topics in arithmetic are as challenging as dividing fractions. And as tough as this topic can be for our students, teaching fraction division can be even more challenging for teachers.

It’s no wonder that so many of us simply teach our students to ‘keep, change, and flip.’ There’s even a cute rhyme about the ennui of teaching fraction division: it’s no use to wonder why, just invert and multiply.

But while these tricks may seem to make our lives easier in the short run, they create hidden problems for us and for our students. 

Looking for resources to help your students develop their fraction foundations? Download your FREE Hands-On Fraction QuickStart Guide

Why Focus on Conceptual Approaches to Fraction Division?

Research on learning and the brain has identified numerous benefits associated with conceptual understanding in math. When students learn math solely through memorization and procedures, many of these benefits are lost.

Conceptual approaches to math have been shown to increase retention, or students’ ability to remember what they’ve learned.

We often think of ‘remembering’ as good, and ‘forgetting’ as bad. But if we remembered everything, our brain would quickly become so cluttered that we couldn’t think.

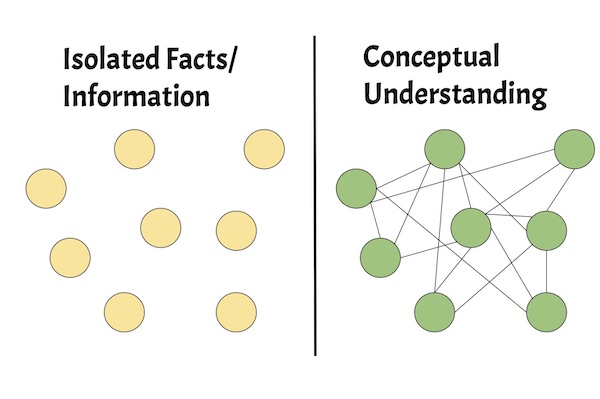
So the brain acts as an efficient gardener, weeding out unimportant memories, so we can make use of the important ones.

So How does the brain decide what matters? By looking at connections. Isolated bits of knowledge are plucked and discarded like weeds, while information that forms a connected web of understanding is deemed important, and thus preserved. 

Conceptual understanding is also critical for application, or students’ ability to use what they learn in novel situations. This includes applying their understanding outside of the classroom, or to increasingly complex ideas they encounter in future grades.

Constructing conceptual understanding is like erecting a building. If you want to build a skyscraper, you start by digging deep and pouring a strong foundation of concrete. Each level must be solid, so it can support all the levels that will eventually be built on top of it.

Relying on tricks is more like building a house of cards. It doesn’t require much of a foundation, and we may feel like we can progress quickly from one level to the next. But such structures aren’t built to last. They may support one or two stories, but sooner or later, the whole thing comes crashing down. 

Resources for Teaching Fractions

Teaching Fraction Division with the 3 Vehicles

So assuming you appreciate the importance of teaching the concepts behind fraction division, the next question is ‘how.’

After all, most textbooks are not designed to build conceptual understanding. They are built on a Content Coverage model of instruction, in which a teacher moves students through uniform content, at a uniform pace. 

There are certainly benefits to exposing students to appropriate grade level content. But to build deep understanding, students need to engage in inquiry-based learning (IBL). To learn through inquiry, we present students with questions, rather than answers. By engaging in productive struggle, and building on what they already know, students develop deep, enduring understanding of math concepts.

With the number of standards to be covered each year, it can be challenging to come up with new hands-on investigations for every topic. But I’ve found that three lesson models, which I call The 3 Vehicles for Conceptual Math, can be used again and again to turn almost any math concept into an inquiry-based activity.

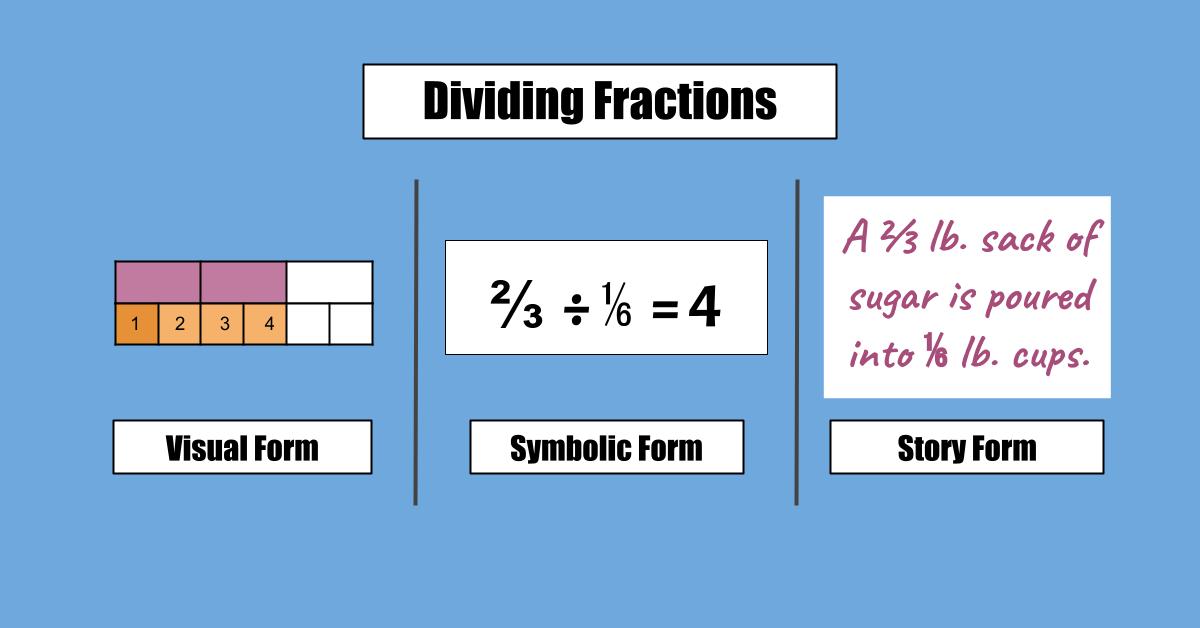
Scale Models: Manipulatives and visual models that reflect the size of numbers and the meanings of operations. 

Number Sentences: Expressions and equations are a great alternative to ‘stacking’ algorithms. Number sentences provide more flexibility and help students develop conceptual understanding.

Stories: Connecting mathematical ideas to real-world situations (aka word problems), helps students attach meaning to mathematics and apply what they learn outside of school.

I usually use scale models to introduce a new math concept, as they are often most effective way for students to understand what a number or operation actually means. Next, I teach them to translate to a symbolic/abstract representation using number sentences.

Finally, we’ll look at story problems involving the new concept. The visual modeling and number sentences become useful strategies for solving the story problems.

The ultimate goal is for students to be able to translate fluently among all 3 vehicles. This is a solid indication that they have mastered the concept.

For more on planning inquiry-based lessons with this approach, check out my previous posts on The Three Vehicles of Conceptual Math and Lesson Plans that Promote Student Engagement.

A Note About Partitive vs Quotative Division

The biggest challenge to teaching fraction division is that many students have gaps in the foundational concepts required to make sense of dividing fractions. Many have been exposed to a ‘tricks-based’ approach to math instruction for several years, and have a shaky, or nonexistent, understanding of both fractions and division.

When students have a solid conceptual understanding of foundational concepts, they can make sense of fraction division by simply combining what they know about fractions, with what they know about division. 

But when I first tried to teach my students to divide fractions, I began to realize that I was missing a key understanding about division myself. In fact, I taught math for several years before I learned the difference between partitive and quotative division. 

The difference comes down to the meanings of the divisor and the quotient. In partitive division, the divisor tells us the number of groups, leaving the quotient to specify the size of each group.

In quotative division, the meanings are reversed. The divisor specifies the size of each group, leaving the quotient to tell us the number of groups.

Most of us intuitively understand division as partitive: dividing by three means to split into 3 groups. But it usually makes more sense to use quotative division when dividing fractions. After all, how do you split something into ⅓ of a group?

As we go through the progression of fraction division, I’ll suggest whether to introduce each stage using partitive or quotative division. For most of us, it’s sufficient to focus on one or the other for each stage. But you may find it a fun challenge to consider how you would use both types for each stage.

For more on division concepts, including partitive vs quotative, refer to Teaching Division for Conceptual Understanding.

Stage #1: Fractional Quotients (Partitive)

I think there are two reasons that fraction division is particularly challenging. The first is that division is itself a challenging operation, which requires a measure of algebraic reasoning. (Think ‘unknown factor.’)

The second reason is that fractions are, themselves, a division problem. Therefore, when dividing two fractions, we are essentially ‘dividing division by division.’ What the what?

This is why it’s so important that before dividing fractions, students have mastered the concept of fractional quotients. In most states, fractional quotients are a 5th grade standard. But I can’t tell you how many middle school students I’ve stumped with an expression as simple as 3 ÷ 4. 

Students should learn that they can define a fraction as the numerator divided by the denominator. But they should also be able to explain why this is, using real world examples and visual or physical models.

Since we are splitting 3 wholes into 4 equal parts, fractional quotients are easiest understood using partitive division.

This Lesson Plan and Activity will help your students develop a conceptual understanding of fractional quotients.

Stage #2: Fraction Divided by Whole Number (Partitive)

Once students understand how a fraction can represent one whole number divided by another, the next step is to divide a fraction by a whole number.

At this stage, we are only dividing by whole numbers that are factors of the numerator. Start by dividing by the numerator (eg, ¾ ÷ 3). This reinforces for students how fractions work – that ¾ is composed of 3 pieces, each of which is ¼. 

Next, move on to numerators that are 2 or 3 times the divisor, such as ‘6/7 ÷ 2’ or ‘9/10 ÷ 3.’ As long as students understand the concepts of numerators and denominators, they can simply divide partitively, as they would when dividing whole numbers.

Stage #3: Whole Number Divided by Fraction (Quotative)

This is the point at which students first start to actually divide by a fraction.

And this was also the point where I used to give up on teaching the meaning behind the math. I was thinking of division partitively, and couldn’t figure out what it meant to split something into ⅓ of a group, or worse yet, ⅖ of a group.

But eventually, my curiosity got the better of me, and I finally figured out that you could divide by repeated subtraction, which is another way of describing quotative division. 

Suddenly, it made so much more sense. If I divide a whole into thirds, of course there will be three of them. And if I draw 2 wholes split into thirds, it’s easy to see that there are 6 pieces.

This process can also be extended to cases where the the quotient is a fraction or mixed number, such a 5 ÷ ⅔.

• I start by taking ⅔ from each whole (5 groups of ⅔).
• That leaves ⅓ remaining from each whole (5 thirds, or 5/3).
• That 5/3 can make 2 more complete groups of ⅔ (7 total so far)
• There is ⅓ left over. That ⅓ is half of a group (half of ⅔)
• We can make a total of 7 ½ groups. 

That’s the process I go through in my head to solve this problem with mental math. The bar model below uses a similar process, but without the regrouping.

Stage #4: Fraction Divided by a Fraction with Like Denominator (Quotative)

Once students have encountered fraction division problems with a fraction in either the dividend or the divisor, they are ready to approach problems with fractions in both the dividend and divisor.

This is much simpler when the dividend and divisor have the same denominator. Examples like ⅔ ÷ ⅓  reinforce the idea that we are dealing with a ‘unit’ of ⅓. Since we can subtract ⅓ away from ⅔ two times, this type of fraction division is best understood as quotative. 

Next, we can move to slightly more complicated examples like 6/7 ÷ 2/7, where students are subtracting 2 units at a time, but which still produce a whole number quotient (3).

Then, students can extend their reasoning, as they did in Stage 3, to examples that produce an intuitive mixed number quotient. If we ask them to divide 5/7 by 2/7, they can take away 2/7 twice before they are left with only 1/7. Since this is half of the divisor, our final quotient is 2 ½.

I find such examples a bit simpler than similar ones that produce a fraction (as opposed to a mixed number). For example, 1/7 ÷ 2/7 would give us a ‘simpler’ quotient of ½. However, the previous example allows students to do something familiar (subtracting 2 copies of 2/7) before something unfamiliar (subtracting half a copy of 2/7). But if you find your students struggling with the mixed number quotients, you may want to try it the other way around.

Stage #5: Fraction Divided by Fraction with Compatible Denominator (Quotative)

Next, students can begin dividing fractions that have ‘compatible denominators.’ These are denominators in which one divides easily into the other, such as halves & fourths, 3rds & 6ths, etc.

At first, the divisor should have the larger denominator, as in ½ ÷ ¼, or ⅔ ÷ ⅙. Students can easily visualize taking away the smaller 6th’s from the larger 3rd’s. And for students still confused by the idea that a larger denominator means a smaller fraction, this practice can help them master that foundational concept.

Then, students can do the reverse, dividing a smaller fraction by a larger, compatible one, such as ½ ÷ ¼. At this point, they can rely on the understanding they developed with fractional quotients (2 ÷ 4) and dividing certain like denominators (⅓ ÷ ⅔) to imagine what happens when we divide one fraction by another that is twice as large – we get ½.

A Note About the Ghost Copies Strategy for Partitive Division

Before moving on the the 6th (and final) stage of fraction division, we will want to revisit partitive division, using a strategy I call ‘ghost copies.’

I came up with this strategy when I hit a wall with using quotative division for dividing fractions. In all the cases described above, it was a fine approach. Instead of wondering how to split ⅗ into ⅕ of a group, I could just use quotative division and subtract ⅕ three times.

But this approach didn’t work for all fractions. If I want to divide ⅔ by 6/7, repeatedly subtracting 6/7 won’t get me anywhere.

It also seemed odd that I could divide whole numbers using either partitive or quotative division, but that fractions could only be divided one way. Part of what I love about math is finding cases where the same rules apply to different types of numbers.

So I thought about what it meant to divide whole numbers partitively, as in dividing 8 into 2 groups. What if, instead, we read it as “8 is composed of 2 groups.” This could make more sense with regards to fractions, as I could read 8 ÷ ½ as “8 is ½ of a group.”

This way of thinking about dividing fractions allowed me to make sense of (and draw) a larger set of fraction division problems.

Stage #6: Fraction Divided by Fraction with Incompatible Denominator (Partitive)

By the 6th and final stage, our students will finally be able to divide any fraction by any other fraction. 

It’s at this point that many of us may decide it’s time to just keep-change-flip and not worry about the meaning or the visual modeling. And if your students can approach stages 1-5 conceptually, they’ll probably be fine just using the algorithm from here on out.

But for those of us with an insatiable curiosity for why math works, we can still incorporate reasoning for finding the more complex quotients.

We can start with a simple example, like ⅕ ÷ ⅓. It looks simple, as both are common unit fractions. But since the denominators are not compatible, it’s hard to repeatedly subtract one from the other. 

We could find a common denominator, giving us 3/15 ÷ 5/15, which is essentially the same as 3 ÷ 5, or ⅗. And while dividing fractions with common denominators is a fine, albeit less common, approach, it’s still more of an algorithm. It doesn’t really tell us what’s happening, and it’s a bear to draw.

Instead, I prefer using a bar model and the ghost copies strategy. I start by modeling ⅕. Then, since ⅕ is ⅓ of a whole group, I line up a model of ⅓ beneath my 5th. By filling in the remaining 3rds in the bottom bar, I show that our quotient (one full group) would be ⅗.

One benefit to modeling these scenarios is that it helps students understand why the ‘keep-change-flip’ algorithm works. Since our divisor is the number of groups, we need to ‘scale up’ our dividend to find the size of 1 group. 

If ⅕ is ⅓ of a group, we multiply by 3 to find the whole group (⅕ ÷ ⅓ = ⅕ x 3). If ⅕ is ⅔ of a group, we need to divide by 2 to find ⅓ of the group, and multiply by 3 to find the whole group (⅕ ÷ ⅔ = ⅕ x 3/2).

Going Beyond: Approximate Modeling

Just for fun, I also like to demonstrate how this approach could be used even for non-intuitive fraction division scenarios. To model 7/16 ÷ 5/9, I start by modeling 7/16, and line up a model of 5/9 below. To find the quotient, I have to extend the “5/9 of a group” to one full group, 9/9. 

I see that the 9/9 on the bottom model aligns roughly to 12.5/16 (25/32) on the top model. When I check my answer with the algorithm, I get 63/80, or 0.7875. The quotient I modeled (25/32) comes out to 0.78125. So this type of model won’t give an exact answer (because I had to estimate where my quotient fell between the lines for 12/16 and 13/16).

One benefit to modeling this type of fraction division is for students to see that 7/16 and 5/9 are both pretty close to ½. And that dividing such fractions should give us an answer close to 1. Another reason is to demonstrate that it is possible to model almost any fraction division scenario.

Online Workshops for Math Educators

Bringing Fraction Division Concepts to Your Classroom

What struck me most about teaching fraction division was how many embedded concepts there are.

When adding and subtracting fractions, the main steps were going from like to unlike denominators. And since multiplication is commutative, multiplying a whole number by a fraction works the same as multiplying by a whole number.

But with division, it seems like each problem requires a different approach. This is why so many students (and educators) struggle when it comes to teaching the concepts and incorporating visual models.

Though it may seem time-consuming, make sure to teach your students the different stages of dividing fractions. This will not only ensure they develop a conceptual understanding of fraction division, it will solidify their understanding of the foundational fraction and division concepts.

What’s more, when you teach the stages in order, students can transition easily from one to the next. You shouldn’t need to spend days introducing, practicing, and reviewing each stage. If your students have limited experience with hands-on, conceptual math, you may need to spend extra time at the earlier stages. But once they develop the foundations, you can pick up the pace.

Classroom Resources and Professional Learning

If your existing classroom resources aren’t doing enough to build conceptual understanding, you can find a wealth of fractions resources in our Online Store.

Ultimately, the 3 Vehicles are meant to help you easily develop problem-based activities for multiple standards. And since our downloadable resources are editable, you can modify them for other standards you are covering, or simply to provide your students extra practice. We also offer virtual workshops on all three vehicles, for both elementary and middle school. To enroll in an upcoming open workshop, visit our workshops page.

If you’re looking to bring more inquiry-based math to your school or district, schedule a free consultation. We’ll talk through your goals and help you decide whether our workshops, coaching, or consulting are the best fit for your needs.

If your students would benefit from a conceptual approach to fraction foundations, download our free Hands on Fractions Quick-Start Guide. It includes teacher resources and classroom resources to build meaningful understanding of fraction basics. You’ll also be added to our weekly Educator’s Newsletter, packed with tips and strategies to bring hands-on learning to your classroom.

Get Your FREE Copy of FRACTIONS QS GUIDE

About the Author

Jeff Lisciandrello is the founder of Room to Discover and an education consultant specializing in student-centered learning. His 3-Bridges Design for Learning helps schools explore innovative practices within traditional settings. He enjoys helping educators embrace inquiry-based and personalized approaches to instruction. You can connect with him via Twitter @EdTechJeff