Patterns and Functions: The Hidden K-8 Math Standards

“Mathematics is the study of patterns.” This quote, attributed to the British mathematician, G.H. Hardy, has been repeated by many. And it’s now widely accepted as one of the definitions of mathematics. Given that math is all about patterns, it’s surprising how small a role patterns and functions play in many math classrooms.

The reason goes back to the adoption of the Common Core State Standards. While not perfect, the CCSS represent an important shift away from thinking of math as simply calculation. There is a greater focus on “numeracy,” the mathematical equivalence of literacy.

The Common Core standards have succeeded in introducing “algebraic thinking” to elementary school math. They’ve also elevated visual models, number sense, and Base-10 understanding. All of these are important foundations for a conceptual understanding of mathematics.

And if you look closely enough, you’ll see patterns and functions hidden behind almost every standard. What is skip counting, if not a simple pattern? And reciting the 5’s times table is the same thing as skip counting by 5. Plugging the number ‘7’ into to the 5’s times tables to generate an output of ’35’ gets to the heart of understanding functions.

So not only are patterns a pillar of mathematical thinking, they’re also woven throughout grade level standards and the mathematical practice standards. Why, then, do we hear so little about patterns and functions in our textbooks and classrooms?

Discovering Patterns and Functions

When, late in my teaching career, I began teaching math, I knew nothing about patterns and functions. I had vague memories of ‘finding the next shape in the pattern’ from elementary school. And I remembered replacing ‘y’ with ‘f(x)’ at some point in high school, but I never knew why.

For most of my teaching career, I taught humanities. I only took one college math class: The Mathematics of Music. My high school calculus courses placed me out of the college math requirement, and I happily avoided taking any “real” math.

After a decade of teaching humanities, I applied for an English position at a great school in Manhattan. But when they offered me the job, the details had changed.

“Would you still be interested if it was mostly math?” I liked the school and the principal, and figured the subject was less important than the work environment.

And in some ways, my inexperience was an advantage. I didn’t know the standards that my students would be tested on. I had attended a Common Core workshop, and I had to teach myself about arrays and number lines.

When my students struggled with the textbook, it forced me to do some research. “Why are we teaching this?” “What did they learn last year?”

It was clear that something was missing from the textbook.. Visual models were presented as ‘just another exercise,’ rather than as a tool for understanding numbers.

I developed my own methods, and used the text less and less. I realized that there was a similar process behind every standard:

Start with a number. Do something to it. Produce another number.

I later realized that this was the basic idea of a function.

Putting Functions in the Spotlight

Looking back, the idea that math is about ‘doing things to numbers’ seems kind of obvious. But I had never really thought about it.

I noticed that many of my students also thought about math this way. They saw patterns in numbers and operations, and made connections between topics.

But there was nothing in the textbook to teach the concept of function to the other students. To these students, math wasn’t fun. It was about memorizing “math facts” and algorithms, not sense-making and connections.

Some of the more procedural students had great memories. They did well in elementary school by memorizing facts and procedures. But as the math became more complex, these students began to display common ‘math ailments.’ Some developed math anxiety. Others concluded they weren’t “math people.”

I realized that patterns and functions were the missing link that could help these students think more deeply about math.

We focused on visual models as a form of mathematical communication. We represent a starting value, an operation, and an ending value.

At first, the procedural thinkers struggled. If I asked them to draw “1/2 x 5,” they would calculate the answer with an algorithm. Then they’d draw two and a half boxes.

But with time, they began creating functional visual models. 5 x 7 became seven hops of five on a number line. They used arrays to show that 6 x 4 is the same as 6 x 2 x 2.

Once they thought in terms of patterns and functions, they learned new topics much more quickly. They could see that multiplication worked the same whether you were working with whole numbers, fractions, or decimals. They saw multiplication as repeated addition, and how division ‘undid’ multiplication.

Where Have All the Patterns Gone?

Many students are exposed to patterns from an early age. But we don’t do a great job of helping students see the important role that patterns play throughout their mathematical journeys.

Patterns are one of the first concepts encounter in Kindergarten. Shape patterns help students see the structure inherent in mathematics. And counting itself is a simple pattern – increase by one.

As students extend their understanding to include skip counting, the patterns are still fairly obvious. But once students transition from skip-counting to times tables, many educators begin referring to operations as “math facts.” This switch is both unfortunate and misleading.

Operations are just shortcuts to counting. Adding allows us to ‘count up’ by leaps and bounds, rather than one number at a time. Multiplication is repeated addition, or the counting of groups. Subtraction and division are the opposites of addition and multiplication.

When students see operations as ‘facts’ rather than patterns and functions, they miss the connections. Thus begins the steady decline from conceptual understanding to memorization. Many students begin to see the conceptual math of their early years as babyish and irrelevant.

Unfortunately, this viewpoint is sometimes reinforced by teachers. Many middle grade educators still believe that stacked algorithms are the only “real math.” I’ve been told that visual models are for students “who can’t handle” the traditional approach.

For many students, this ‘conceptual desert’ in their math education ends with Algebra. By high school, the thinking goes, students will have “mastered the basics.” Only then can they be allowed to start thinking in math class.   

Loss of Function

It’s interesting that when functions are finally introduced, little attention is given to the concept. In 8th and 9th grades, the focus is on function notation. Or distinguishing functions from non-functions.

The loss of function (pun intended) in the middle grades is doubly unfortunate. First, because this is the point when many students decide that math is boring, or that they are not good at math.

Second, the power of functions could be harnessed to introduce dozens of concepts. Times tables, ordered pairs, and proportions are just a few topics that make more sense when taught in terms of patterns and functions.

In Marilyn Burns’ About Teaching Mathematics, she devotes a chapter to Patterns, Functions, and Algebraic Thinking:

Patterns are key factors in understanding mathematical concepts. The ability to create, recognize, and extend patterns is essential for making generalizations, seeing relationships, and understanding the order and logic of mathematics. Functions evolve from the investigation of patterns.   -Marilyn Burns

She offers a number of amazing activities to help students develop their understanding of patterns and functions. I’ve used these activities dozens of times with my students, with great results. But it took me a while to really understand how patterns and functions were connected.

Making the Connection Between Patterns and Functions

The first step in connecting patterns to functions is to assign a value to each term. For example, as students skip count by 3s, begin numbering the terms such that term 1 is 3, term 2 is 6, and so forth. Later (in Algebra), students will connect this to the concept of an “nth term,” and represent patterns with sequence notation.

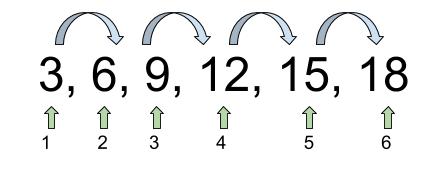
So the major difference between pattern and function is like taking the stairs versus the elevator. If we skip count by 7’s, we can only get to the 40th term by counting from the first through the 39th. But if think in terms of a function, we can think of our function as “times 7.” If we input 40, we can go straight to the 40th term, which is 280.

Three Strategies for Teaching Patterns and Functions

As educators, understanding the value of patterns and functions is important. But seeing the value isn’t enough to teach patterns and functions to our students.

It can be helpful to explain the concepts to our students. But it is even more valuable for students to discover the connections through engaging, inquiry-based lessons. For more on creating lesson plans that promote inquiry, read this article. 

Unfortunately, few textbooks provide the resources needed to teach through hands-on exploration. Most texts break concepts into disconnected bits of information, rather than emphasizing connections. They also ask students to perform too many repetitions of exercises that lack rigor. 

To teach concepts, it’s better to have students focus on a few problems per lesson. Rather than multiple choice or fill in the blank problems from your textbook, consider these activities.

1. Visual Models

Seeing is understanding. By incorporating visual models, we can literally help students ‘see’ the patterns within numbers and operations.

While some believe that visual models are for young students, that couldn’t be farther from the truth. The more complex the mathematical idea, the more helpful it is to have a visual model.

Students who are adept at creating whole number visual models can apply their understanding to more challenging numbers. Area models are great for introducing fractions and decimals. And number lines are a great tool for introducing negative numbers. Students can even use algebra tiles to create physical representations of variables and equations.

 

One challenge to teaching with visual models is understanding how they build off each other. I’ve found that visual models support four progressions of understanding:

• Counting and Base-10,
• Additive,
• Multiplicative
• Patterns/Functions

To teach effectively with visual models, it helps to know which progression you’re supporting. We also need to know where are students are along the way. More on that here.

It’s also important that students don’t just watch us create visual models or see them on worksheets. They also need to create their own. Graphic organizers like this one can help your students make visual models that tell a mathematical story.

2. The Sieve of Eratosthenes

Eratosthenes was a Greek mathematician seeking an efficient way to find prime numbers. Before him, mathematicians looked for prime numbers by picking a number and trying to find a number you could divide it by.

Eratosthenes decided to go the other way. He realized that by skip-counting, you could much more efficiently find primes by process of elimination.

Today, the Sieve is a useful tool for helping students see patterns in numbers and develop fluency with times tables, adding and subtracting, factors, and more.

This lesson plan uses the sieve to help students see patterns in the times tables. First, they pick a color for each single-digit number. Then, they put an ‘x’ in each multiple of that number up to 100. Then, they complete a notice and wonder chart about the patterns they find in the table.

I recommend conducting this lesson with students at any age. You’ll be amazed at how much older students gain from seeing patterns in a hundreds chart. And even students who haven’t learned their times tables yet can connect it to counting, adding, and subtracting.

3. Function Machines

Number lines, arrays, and sieves can help students see patterns in numbers. The next step is to apply function understanding to these patterns. Then, students can skip to any term in a pattern without completing the entire sequence.

Function machines are an excellent way to help students to make this connection. A function machine is basically a table with two columns. Every time you put a number in the left column, another comes out on the right.

The columns can be labeled “in/out,” “x/y,” or “box/triangle.” The “machine” can perform a single operation, such as “multiply by 3,” or a series of operations.

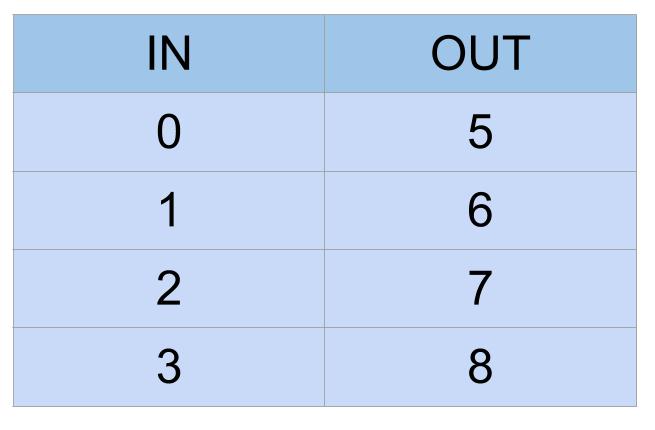
Once we introduce function machines with whole numbers, we can extend to more advanced numbers.

For example, to introduce negatives, ask your students, “With a ‘plus 5’ function machine, how do we get an output of 1?” This approach can also introduce decimals and negatives.

Eventually, students can use non-counting numbers as inputs. This helps them see that operations work generally the same way with all categories of numbers. For example, a ‘times 7’ machine would show that 10 x 7 is 70, and .01 x 7 is .07.

Such generalizing is a crucial element for introducing variables. Once students see that an ‘in-out machine’ multiplies by 3 and adds 7, it’s a small step to think of the input as ‘x’ and the output as ‘y.’

This Multiple Representations of Functions Organizer can help students see the same function relationship in multiple forms. It includes sections for a table (function machine), graph, equation, and story. Fill in one or two of the sections, and have students complete the rest.

Make Math Engaging with Patterns and Functions

Teaching students about patterns and functions can increase their enjoyment of math, as well as their achievement.

Students who are fluent in patterns and functions have a tremendous advantage over those who don’t. Students who only know facts and algorithms may appear successful, but they are not developing the ability to generalize their understanding. As they get older, their inefficient approach forces them to work harder and harder to keep up. In order to be successful in Algebra and beyond, they must develop their mathematical reasoning.

While they are not mentioned as explicitly in the grade level standards, patterns and functions play a central role in the oft-overlooked ‘Standards for Mathematical Practice.’  These eight standards define the elements of mathematical thinking that cross grade levels. SMP7 and SMP8 address the ability to “make use of structure” and employ “repeated reasoning.”

Are your students fluent in finding patterns and understanding functions? Would you like to help them, but don’t know where to start? You can connect with other innovative educators in our Facebook group. The Reflective Teacher’s Community is dedicated to bringing creativity, collaboration, and conceptual learning to every student in every classroom.

For more teaching tips and innovative ideas like this one, subscribe to our free Educator’s Newsletter. Each week, we share posts like this one with educators like you. Sign up to get a weekly dose of education inspiration, straight to your inbox.

GET THE FREE NEWSLETTER

About the Author

Jeff Lisciandrello is the founder of Room to Discover and an education consultant specializing in student-centered learning. His 3-Bridges Design for Learning helps schools explore innovative practices within traditional settings. He enjoys helping educators embrace inquiry-based and personalized approaches to instruction. You can connect with him via Twitter @EdTechJeff